Oscar De Wit is a PhD student at the Cantab Capital Institute for the Mathematics of Information (CCIMI). This article is based on a talk by Oscar’s talk at the CCIMI Industry Engagement Day which took place on 23 November 2022, hosted by the Newton Gateway to Mathematics. You can watch a video of the talk here.

Thank you to our colleagues at Plus Magazine for allowing us to reproduce their article on the CCIMI website.

Ants seem to effortlessly cooperate and work together. Just think of how ants travel in well-ordered lanes carrying food back to their nest, all done without any sort of agreement or master plan.

Individual ants don’t leave their nest with explicit instructions for where to go or how to get there. Instead they respond to their urge to find food for their colony, the movement of their very closest neighbours (they have terrible, and in some cases non-existent, eyesight) and the chemical trails of pheromones all ants leave behind them as they move. (You can find out more about how ants interact, and the power of mathematically capturing this behaviour, in The power of ants.)

“What I like about this video is the ants follow each other in a structured pattern,” said Oscar de Wit in his talk at the Connecting with Industry event organised by the Cantab Capital Institute for the Mathematics of Information (CCIMI) and the Newton Gateway to Mathematics. “They’re walking along in a lane, some in the opposite direction. There’s this persistent, collective, ant behaviour. How can we understand this? How can we study this scientifically?”

Average your ants

Mathematics has been used to investigate how surprising patterns such as this emerge in the collective behaviour of large groups of animals, such as flocks of birds or schools of fish. De Wit is using a similar approach. Mathematically each individual ant is thought of as a particle, with a certain position and orientation at a particular time, that interacts with the other particles as it moves over time according to simple mathematical rules.

You might think you’d have to simultaneously keep track of each and every ant in order to simulate how they’d move as a group over time. But luckily, a mathematical technique called the mean field limit makes things much easier. Essentially you average the effects felt by a single ant, from all the other ants, as you let the number of ants in your group become very large, approaching infinity. (This might seem like a surprising approach, but seeing what happens to a mathematical expression as a quantity goes to infinity is a common tool in maths. Find out more in our brief introduction to limits.)

This mean field limit of your equations gives you an approximation of the behaviour of an “average” ant in your group. “Roughly it gives you the probability of finding an ant at a particular position and in a particular orientation at a time t,” says de Wit. (You can see an illustration of how this is used in the images, below, from one of de Wit’s simulations.) It is now much easier to use this mean field limit to simulate how a group of ants would move over time, starting from a random assortment of positions and orientations. (You can find out more about how maths has been used to understand systems made up of many components, in Kinetic Theory: Taming multitudes.)

Looking ahead

We could try to include everything we know about ants when we write down the mathematical rules for how they interact. “Ants are very complicated,” says de Wit. “But maybe we should focus on one thing that we know. What is the [simplest] mathematical model that captures ants forming lanes, or other collective [behaviour]?”

De Wit instead focuses on the orientation of the ants and how each ant is affected by the pheromones left in the space around it by the other ants. His initial approach placed this alignment mechanism at the centre of the ant, combining its current orientation with the direction of the strongest signal (called the gradient) from traces of pheromones around it. Although this mechanism did result in an interesting behaviour of “ant spots” forming, he pushed his model further.

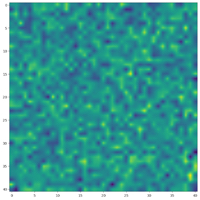
De Wit started his simulation with ants scattered randomly across the space. The colours represent the probability of finding an ant at each point in the space – the more yellow, the likelier it is to find an ant at that spot.

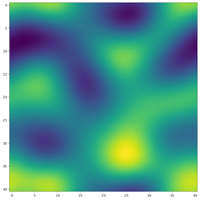
Part way through his simulation, the ants are still moving about the space.

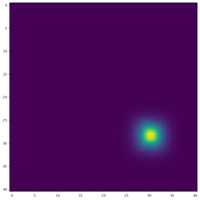
After some time the ants have stopped moving, as they have all clustered together in an “ant spot”. (Images by Oscar de Wit – used with permission)

Instead of calculating the strongest pheromone signal from the centre of the ant, the new approach, developed by de Wit together with his supervisor Maria Bruna and researcher Ulrich Dobramysl, calculated it at a point just a little further in front – you can think of this point as positioned at the antenna of the ant. “This is a kind of shift in their sensing,” says de Wit. “It gives much more interesting behaviour.” When they ran this simulation of the ant’s movement, starting with dropping ants into the centre of the space at random orientations, lanes of movement formed over time.

Just this small change in where an ant detects its surroundings seems to result in far more interesting behaviour. De Wit is now exploring what mathematical results he can prove for this more complicated model, such as what sort of lanes can form and how stable these structures are over time. “Modelling ants is very interesting because it requires coming up with new mathematics that can then also be used to study other models with other interesting emergent behaviour,” he says.

What’s new in data science

De Wit is a PhD student at the Cantab Capital Institute for the Mathematics of Information (CCIMI) , based at the University of Cambridge. The CCIMI explores how maths can be used to understand the wealth of data and information around us. Complex systems, like a colony of ants self-organising to form ordered patterns, may one day help us find new ways to unearth information hidden in large data sets. Altogether five CCIMI PhD students showcased their work to researchers and industry partners at the Newton Gateway event. The range of work on show demonstrated the breadth of PhD research happening at the CCIMI – from Hong Ye Tan’s work on machine learning in image reconstruction to Vali Lungo’s use of Markov chains to study the structure of DNA.

“The aim of the day is to get to know the exciting maths problems people face in industry, and for industry to see some of the new mathematics,” said Randolf Altmeyer, CCIMI researcher and Deputy Director of the PhD programme. It was exciting to see the new mathematics being done by CCIMI researchers such as John Aston, and leading industry experts, alongside PhD students doing their first research in the field. “The CCIMI is a PhD driven programme,” said Altmeyer. “We want to generate the new leaders of the field.” We look forward to seeing where these CCIMI students will take the field next.

About this article

This article is based on a talk by Oscar de Wit’s talk at the CCIMI Industry Engagement Day which took place on 23 November 2022, hosted by the Newton Gateway to Mathematics. You can watch a video of the talk here.

Rachel Thomas is Editor of Plus.

This article was produced as part of our collaborations with the Cantab Capital Institute for the Mathematics of Information (CCIMI), and the Isaac Newton Institute for Mathematical Sciences (INI).

The INI is an international research centre and our neighbour here on the University of Cambridge’s maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.